Linear Discriminant Analysis LDA - Using Linear regression for classification

Linear Discriminant Analysis LDA uses linear regression to supervise the classification of data. Essentially you assign each class a numerical value. Then use linear regression method to calculate the projection of your observations to the assigned numerical values. Finally you calculate the thresholds to distinguish between classes.

Essentially LDA attempts to find the best linear function that separates your data points into distinct classes. The above diagram illustrates this idea.

Implementing LDA using LAMBDA

Fit

Steps in implementing LDA's Fit:

1. Find the distinct classes and assign each with an arbitrary value - UNIQUE and SEQUENCE.
2. Designate each observation with the arbitrary assigned value depending on its class - XLOOKUP.

3. Find the linear regression coefficients for this observations - dcrML.Linear.Fit.

4. Project each observation on the linear regression - dcrML.Linear.Predict.

5. Find the threshold of each class - classCutOff from the spread of each regressed class.

6. Return the linear coefficients and thresholds.

Below is the implementation.

dcrML.LDA.Fit
=LAMBDA(arrayData, arrayClass, [dataHeaders], [showDetails],
  LET(
    classNames, UNIQUE(arrayClass),
    classIndex, SEQUENCE(COUNTA(classNames)),
    classValues, XLOOKUP(arrayClass, classNames, classIndex),
    linearCoeff, dcrML.Linear.Fit(classValues, arrayData, FALSE),

    linearPredict, dcrML.Linear.Predict(linearCoeff, arrayData),
    classMean, BYROW(classNames, LAMBDA(pRow, AVERAGE(FILTER(linearPredict, arrayClass=pRow, 0)))),
    classSize, BYROW(classNames, LAMBDA(pRow, COUNT(FILTER(linearPredict, arrayClass=pRow, 0)))),
    classMeanXSize, classMean * classSize,
    classSizeShift, DROP(classSize,1),
    classMeanXSizeShift, DROP(classMeanXSize,1),
    classCutOff, (classMeanXSize + classMeanXSizeShift)/(classSize + classSizeShift),

    details, IF(showDetails,
      HSTACK(
        VSTACK("Class", classNames),
        VSTACK("Cut Off", classCutOff),
        VSTACK("Linear Coefficients", linearCoeff),
        VSTACK("Idx", classIndex),
        VSTACK("Class Idx", classValues),
        VSTACK("Predict", linearPredict),
        VSTACK("Class Mean", classMean),
        VSTACK("Class Size", classSize),
        VSTACK("Class MeanXSize", classMeanXSize),
        VSTACK("Class Size Shift", classSizeShift),
        VSTACK("Class MeanXSizeShift", classMeanXSizeShift)
      ),
      HSTACK(classNames, classCutOff, linearCoeff)
    ),
    IFNA(details,"")
  )
)

Predict

The LDA Fit results is then used to Predict the class of data observations arrayData, using the input parameters of the class names arrayClass, class thresholds arrayCutOff, and linear coefficients linearCoeff.

Below is the implementation in Excel LAMBDA.

dcrML.LDA.Predict
=LAMBDA(arrayClass, arrayCutOff, linearCoeff, arrayData, [showDetails],
  LET(
    class, DROP(arrayClass,-1),
    lastClass, CHOOSEROWs(arrayClass,COUNTA(arrayClass)),
    linearPredict, dcrML.Linear.Predict(linearCoeff, arrayData),
    ldaPredict, XLOOKUP(linearPredict, arrayCutOff, class, lastClass, 1),
    details, IF(showDetails,
      HSTACK(
        VSTACK("Linear Predict", linearPredict),
        VSTACK("Class Predict", ldaPredict)
      ),
      ldaPredict
    ),
    IFNA(details,"")
  )
)

Let's see this in Action

Fit

We will use the Iris data to demonstrate the Lambda implementation of LDA. The Fit function takes the numerical data for linear regression and the class data as the supervised input. Below shows the results of dcrML.LDA.Fit.

NOTE: The Iris data that I use is shuffled (i.e. not grouped by classes). This was intentional so as to prevent patterns arising from sequentially ordered data, which could lead to overfitting. Overfitting occurs when a model learns too well from the training data and unable to predict accurately with new data.

Predict

The LDA Predict is used predict the classes for new data.

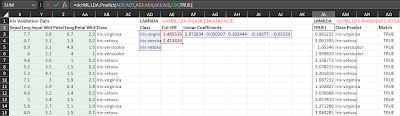
The example below shows the input validation data on the left. In the center are the Fit output parameters. On the right shows Predict using both the aforementioned data as inputs. Because I used the showDetails = TRUE parameter, the returned results have 2 columns: one the linear regression values and the other the class prediction. The far right is a manually created column to compare the input data classes against the predicted classes. The validation accuracy for this fitting happens to be 100%.

NOTE: For validation, the Iris data used is distinct from the training data. The purpose of doing this is to cross validate the model. If the model learns too well from the training data then there is no way to confirm the model's accuracy.

Questions and Answers

What are some of the weaknesses of LDA?

When observation classes are too close to each other, the threshold would be marginally different. This may not be sufficient to contrast the linear projection of the observations. When facing this, you will have high rates of false positives.

LDA may be too simplistic. It assumes a single dimension is sufficient to describe a class regardless of the number of features.

Would assigning a larger class values help?

No, it won't. What is required is to accentuate the difference between the classes. This may not be possible with linear regression if the classes are highly overlapped. In such cases logistic regression would be a better approach. Logistic regression uses sigmoid functions to achieve good separability.

Conclusion

Linear Discriminant Analysis LDA is an example of supervised classification technique using linear regression, and I have shown its implementation using Excel Lambda.

Go forth and discriminate your data with DC-DEN!